
Один из вопросов, стабильно вызывающий непонимание у широкой общественности, – вопрос целеуказания при стрельбе противокорабельными управляемыми ракетами (ПКР). И именно непонимание этого вопроса приводит к тому, что наши люди активно верят в сверхоружие. Ещё бы, ракета может поразить корабль с тысячи километров!
Может. А может и не поразить. Чтобы поразить, ракета должна, пролетев эту самую тысячу километров, выйти на цель с необходимой точностью. А если текущее место цели на момент пуска известно со значительной ошибкой? В этот момент любопытствующие начинают делаться на тех, кто способен мыслить рационально, и тех, кому для ремонта пошатнувшихся устоев сразу же нужна какая-то сказка. Спутники, например, которые видят цель и «передают» что-то куда-то, после чего из этого «куда-то» точно в цель прилетает несбиваемая ракета. Или гигантский сектор захвата ГСН ракеты, на многие десятки километров, вместе с её якобы сверхманёвренностью, которая позволит дать вираж за целью и не промахнуться.
В реальном сложном и опасном мире всё иначе. И, дабы не давать себя дурить, всем причастным стоит разобраться с этим самым целеуказанием.
Прежде чем мы пойдём дальше, проясним несколько важных нюансов. Этот текст – популяризаторский, это не цитирование рукдоков или «Правил ракетной стрельбы». В нём простым разговорным языком и на элементарных примерах разъясняются базовые понятия. Более того, даже с учётом этого многое просто оставлено за кадром, причём специально. Некоторые методы получения данных для этого самого ЦУ просто намеренно не упомянуты. И, как следствие, указания на грубые ошибки от товарищей, носивших чёрную форму, будут восприняты с благодарностью, а вот детализировать и дополнительно разъяснять ничего не надо, это не тот случай, тема слишком серьёзная. Но начнём мы с несерьёзной истории.
Целеуказание Розового Пони
Жил-был Розовый Пони. Он был патриотом и любил свою страну. Но, увы, не любил думать — совсем. И ему казалось, что в мире всё очень просто.

Вот, например, надо всадить ракету во вражеский авианосец.
Ну так какие проблемы, увидели авианосец со спутника и отправили к нему ракету. «А как же ЦУ?» — спрашивали у Розового Пони люди. «Ты что, не видишь? — Розовый Пони показывал копытом на фотографию авианосца со спутника. — Что тебе ещё надо? Видно же цель!»
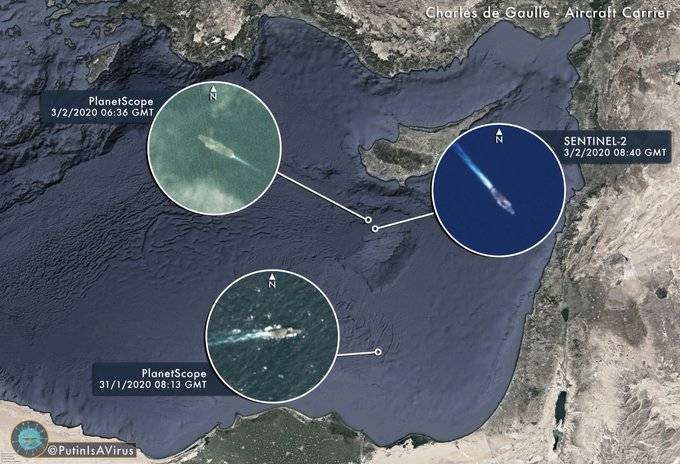
А люди недоумевали и говорили ему: «Так это ты понимаешь, что это «Шарль де Голль» у Кипра, ракете-то как это объяснить?» А Пони начинал бесноваться, громко ржать и кричал на людей: «Да всё уже давно решено, любой нормальный спутник может координаты обнаруженной цели передать куда надо!» Люди не унимались и спрашивали дальше: «Координаты? А их хватит? Что вообще такое целеуказание, ты знаешь? Какой смысл у этого слова?»
Тут Пони приходил в ярость. Он начинал обзывать людей солженицыными и резунами, обвинял их в том, что они за Америку и продались Госдепу: русофобы, поливают свою страну помоями и вообще ничего не понимают! Он писал им в интернете разные глупости и ставил в конце этих глупостей смайлики с высунутыми языками, думая, что вот именно так его глупости ну очень убедительно смотрятся.
Но на самом деле пони просто не хотел думать. Он так и не узнал, что такое целеуказание, хотя ему говорили. Он не слышал. Он думал, что все, кто не такие, как он, не патриоты и враги.
Так что же это такое, целеуказание?
Расскажем об этом кратко.
Данные для стрельбы
Прежде чем двигаться дальше, стоит понять, какие основные данные используются при ракетной стрельбе по цели, которая не наблюдается непосредственно с носителя ракетного оружия.
Представим себе картину. Идёт некая война где-то, а мы, как какой-нибудь хусит, сидим на берегу с самодельной пусковой установкой, на которой стоит вытащенная с разбитого флотского склада ПКР. Мы нашли способ сделать так, чтобы она стартовала и даже можем какие-то команды ей запрограммировать, например, сделать так, чтобы она легла на заданный нами курс, включила ГСН «по таймеру» или сразу, не важно. Теперь, чтобы её запустить, нам надо найти как-то цель там, за горизонтом.
РЛС у нас нет, но есть маленький катер с наблюдателями и радиостанцией. Он ходит по назначенному району «змейкой» и ведёт поиск целей визуально. И вот его экипаж увидел на горизонте боевой корабль. Взгляд в мощный бинокль, силуэт вроде опознан («вроде» – ключевое слово, тут у нас начинается теория вероятности, но о ней чуть ниже). Теперь надо как-то сообщить на берег о том, где цель, причём так, чтобы они сразу поняли, где она, и поняли точно. Море пустое, ориентиров в нём нет. Поэтому для того, чтобы передать «куда надо» данные о цели, надо договориться о том, как объяснить местоположение цели. А для этого нужна система координат. Не существует никакого ЦУ без системы координат.
Системы могут быть разные. Первая – полярная, или относительная.
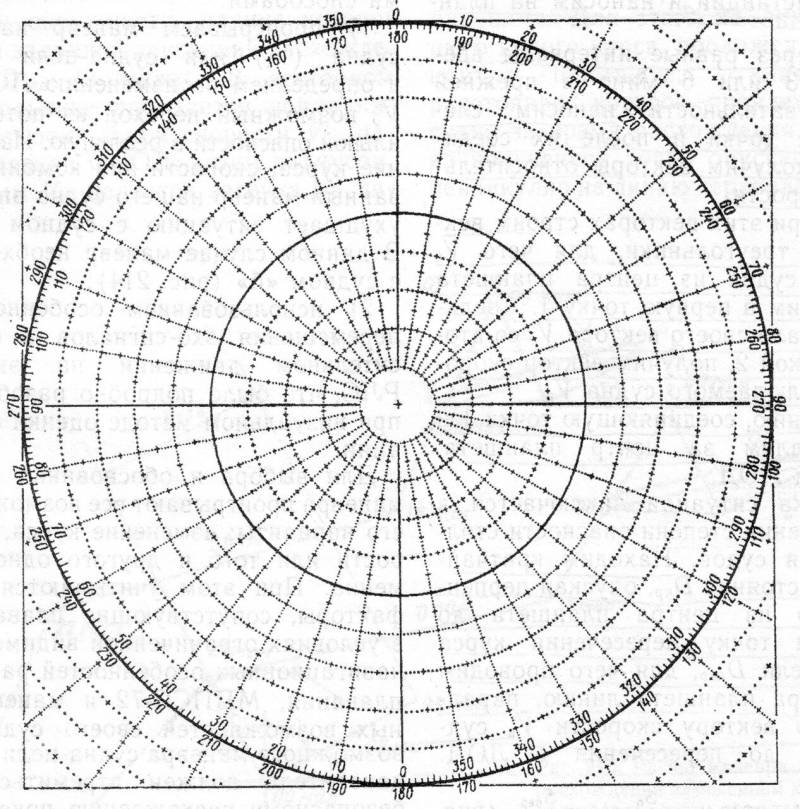
В полярных системах координат есть центральная точка отсчёта, относительно которой задаются положения других объектов. Как правило, это сам объект, ориентирующийся в этих координатах, например, корабль. Он стоит в центре системы координат. Положение других объектов задаётся через угол и дальность. Направление от центральной точки на объект, координаты которого нужно знать (цель в нашем случае) называется словом «пеленг». Дальность даётся по этому пеленгу.
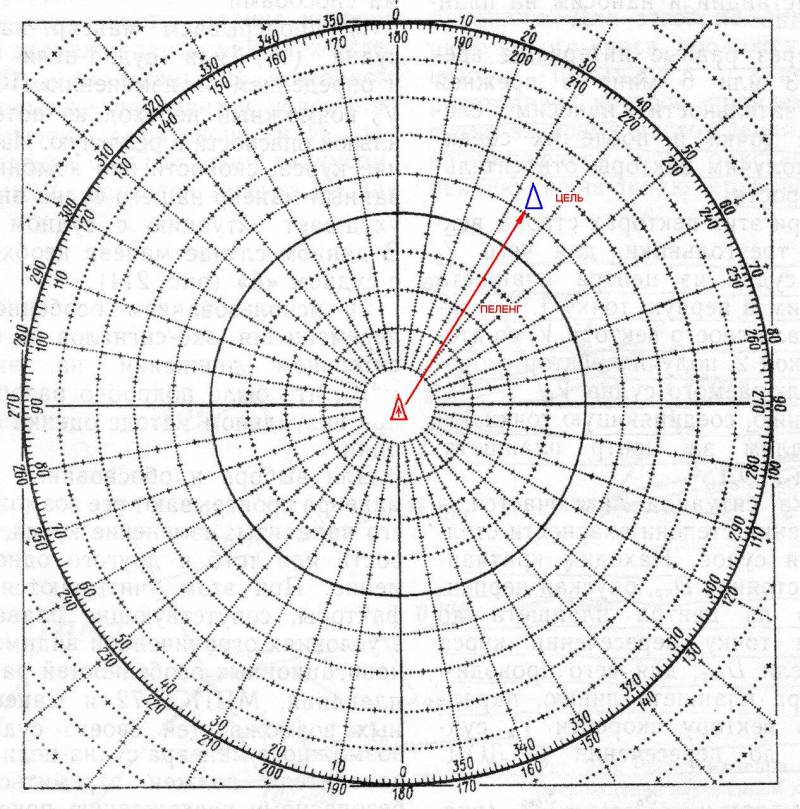
Вторая система — прямоугольная, или географическая. Это обычные географические координаты: широта и долгота. Можно пересчитать данные о положении цели из одной системы координат в другую.
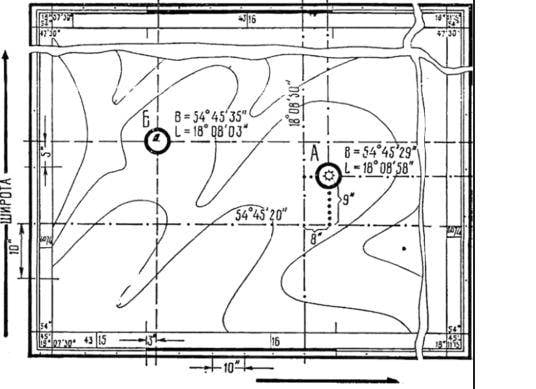
Как нашему катеру передать координаты? Будь у нас автоматизированная система выработки данных для ракетной стрельбы, он дал бы нам пеленг от себя на цель и дальность до неё, а автоматика уже превратила бы два этих числа в пеленг от пусковой установки и дальность от пусковой установки до цели по этому пеленгу.
Но никакой автоматизированной системы у нас нет, поэтому на катере, зная свои координаты, посчитали примерные координаты цели в обычных географических координатах и по радио сообщили на КП пусковой установки. Ничего, мы пересчитаем, если надо, так? Так.
И вот у нас есть координаты цели, а, следовательно, пеленг на неё и дальность.
Данные о точном расположении цели в настоящий момент времени называются "Настоящее место цели" — НМЦ.
Допустим, мы получили эти данные без задержек, быстро пересчитали в относительные координаты, получили пеленг на цель и дальность по нему, потом рассчитали угол поворота ракеты после старта, чтобы её курс совпал с этим пеленгом, запрограммировали это всё в ракету… у нас ушло на всё равно пять минут.
Можно ли отправить ракету точно в НМЦ?
Корабль не стоит на месте, он движется. За пять минут на подготовку к пуску, которую мы выполняли с помощью отобранного у противника ноутбука с «ломаным» ПО, корабль прошёл какое-то расстояние. Более того, пока к нему будет лететь наша ракета, он продолжит идти и пройдёт ещё большее расстояние.
Каким оно будет? Всё просто, оно будет равно времени с момента обнаружения и получения НМЦ и до момента подлёта ракеты, умноженному на скорость цели. А в какую сторону он пройдёт это расстояние? Если мы после обнаружения корабля более его не наблюдаем, то в любую ненаблюдаемую. Например, если корабль ушёл от нашего катера за горизонт, то он может идти или вдоль горизонта в любую сторону, или под углом к нему. В итоге зона, в которой может оказаться корабль, за некое время будет образовывать полукруг. А если наш катер вынужден был от корабля в панике бежать на 45 узлах? И его связь при этом была задавлена корабельными средствами РЭП? Тогда оказывается, что корабль из НМЦ мог уйти в любую сторону, и зона, в которой он может находиться сейчас, являет собой круг.
Эта фигура, внутри которой цель может находиться к данному моменту времени, называется "Область вероятного места цели" – ОВМЦ. К моменту, когда вокруг нашего НМЦ вырос кружок ОВМЦ на карте, оно уже не настоящее, а начальное.
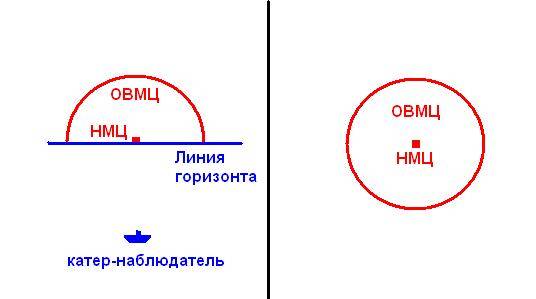
Тут надо сделать оговорку. Если бы у нас была какая-то ещё информация о том, куда может пойти цель, то мы бы превратили круг или полукруг в сектор. Если бы вариантов того, куда пойдёт цель, было много, а у нас было бы время и соответствующее программное обеспечение, то мы бы могли внутри этой ОВМЦ получить распределение вероятностей нахождения цели в той или иной части ОВМЦ. В реальности именно к этому и стремятся, это облегчает стрельбу. Но мы продолжим так, как будто не знаем больше ничего.
Если мы такое распределение вероятностей получить не можем, то для нас критично то, насколько этот круг больше или меньше, чем ширина полосы захвата цели ГСН нашей ракеты. Что если ОВМЦ в два раза больше, чем ширина полосы обзора ГСН нашей ПКР? Шансы на то, что последняя ракета уйдёт «в никуда», становятся весьма велики. А если ОВМЦ не успела «вырасти» и почти вся накрывается полосой поиска ГСН? Тогда более-менее можно стрелять, хотя это всё же риск: ракета может захватить цель где-то на краю сектора обзора, но из-за скорости не успеет на неё довернуть. Чем скоростнее наша ракета, тем точнее мы должны вывести её на цель. Или надо задавать ей большую высоту полёта, с большим радиогоризонтом, чтобы она обнаружила цель с большого расстояния и довернула на неё без проблем, но тогда она будет легче сбиваемой. В идеале – успеть к моменту, когда ОВМЦ ещё небольшая.
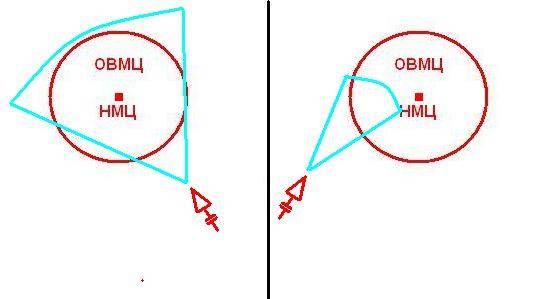
Таким образом у нас возникает зависимость от фактора времени.
Время с момента обнаружения цели до подхода к ней ракеты на дальность действия ГСН называется полным временем устаревания данных.
Это время может быть рассчитано заранее, так как состоит из таких известных величин, как время с момента обнаружения цели до конца передачи сообщения о ней на «стреляющую» единицу (береговая ПУ в нашем случае), время на предстартовую подготовку, подлётное время и т.д. Для корабля в него может входить даже время на какой-то необходимый для пуска ракеты манёвр.
Наша задача — поразить цель, таким образом, сводится вот к чему: полное время устаревания данных о цели должно быть таким, чтобы за это время цель не успела уйти слишком далеко и чтобы размеры ОВМЦ не выросли до превышающих ширину полосы захвата ГСН.
Рассмотрим на конкретном примере.
Допустим, у нас есть корабль, вооружённый ПКР с большой дальностью стрельбы, и нам только что сообщили координаты цели, которую надо поразить, тоже корабля. Дальность до цели – 500 километров. Скорость ракеты на курсе – 2000 км/ч, ширина полосы захвата ГСН – 12 километров. Время с момента поступления на атакующий корабль координат цели до пуска ракеты – 5 минут. Подлётное время очевидным образом 15 минут, полное время устаревания данных – 20 минут, или 1/3 часа. Курс ракеты проложен прямо в НМЦ. Чтобы при подходе ракеты к цели ГСН могла захватить её, нужно, чтобы цель не ушла от НМЦ далее чем на 6 километров по перпендикуляру к курсу ракеты в любую сторону. То есть цель не должна идти быстрее, чем 18 километров в час, или 9,7 узлов.
Но боевые корабли не ходят с такой скоростью. Современные боевые корабли имеют скорость экономичного хода в 14 узлов и максимальную в 27-29. Старые корабли ходили экономичным ходом 16-18 узлов и имели максимальную скорость в 30-35.
Конечно, корабль может идти не поперёк курса подлетающей ракеты, а лагом (под углом) к нему. Тогда он может оказаться в зоне обнаружения ГСН даже идя с высокой скоростью. Но может и не оказаться, и чем больше расстояние до цели (а значит, и полное время устаревания данных), тем меньше шансов попасть в цель, если у нас есть только НМЦ, то есть однократно полученные координаты цели.
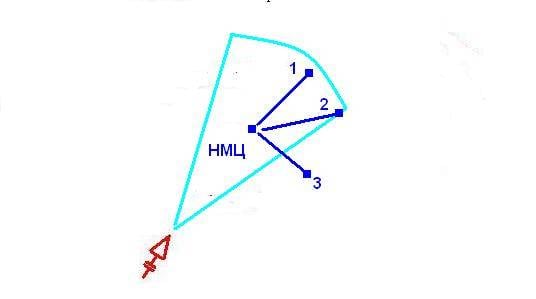
Тут нам надо отвлечься от простых вещей и сказать вот что. На самом деле ситуация ещё сложнее.
В описанных выше примерах отсутствует то, что есть в реальности. Так, например, по отношению к координатам цели должен выполняться расчёт погрешностей, и реально НМЦ мы знаем неточно – это всегда так. Второй момент – вероятности. Результаты подобных задач оцениваются с помощью аппарата теории вероятности. Базовые вещи можно посмотреть в «букваре», известном любому лейтенанту – в книге Елены Сергеевны Вентцель «Введение в исследование операций». Зачем нам теорвер? Затем, что, например, рано или поздно ракета не стартует из ТПК при прохождении команды. Или у неё сломается ГСН. Или рядом с целью окажется круизный лайнер. Противник может буксировать ложную цель рядом и ракета уведётся на неё. Или… и требуемую высокую вероятность поражения цели надо обеспечить именно в таких условиях, когда исход каждого шага по подготовке к пуску, самого пуска, полёта ракеты и поражения цели при успешном выходе на неё носит вероятностный характер. Более того (вспоминаем то, что с катера «вроде» бы опознали цель), даже само обнаружение может быть ошибочным, то есть оно тоже имеет вероятностный характер. При определённых с погрешностями координатах цели при этом. Более того, в реальности даже поправки на ветер надо учитывать, и при пуске на большую дальность их влияние прямо пропорционально дальности.
В таких условиях вероятность успешного поражения цели при стрельбе в НМЦ становится слишком низкой, и стрелять так нежелательно.
Собственно, на этом и спотыкается наш Розовый Пони. Он не может понять, как так: фотка со спутника – это не ЦУ даже в принципе. И понять, почему просто по координатам нельзя отправить ракету, он не может тоже. Но задорно спорит с теми, кто понимает и знает.
А можно ли придать ракете такую скорость, чтобы полное время устаревания данных стало очень небольшим? Вообще, да. Например, если бы в описанном выше примере стрельбы с ракетного корабля по цели на дальности 500 километров скорость цели была бы не 2000 км/ч, а 6000 км/ч, то корабль-цель ни на какой реалистичной скорости из 12-километровой полосы не ушёл бы, но тут была бы другая проблема: такая скорость — это гиперзвук с разными весёлыми эффектами типа плазмы на обтекателе ГСН. А это значит, что у нас не было бы 12 километров…
Или представим себе стрельбу ракетой «Кинжал» на дальность 2000 километров, как обещают по телевизору, причём по кораблю. Для того чтобы подыграть «Кинжалу», МиГ-31К у нас не на аэродроме, а в воздухе – ждёт вражеский авианосец сутки напролёт. Примем, что с момента ЦУ (мы пока не разбирались что это, но не важно) и до того, как МиГ-31К взял курс на цель и набрал скорость, необходимую для отцепа ракеты, прошло 5 минут. Затем ракета уходит на цель. Пренебрегаем её временем разгона, для упрощения считаем, что он мгновенный. Далее имеем полёт на 2000 км со скоростью примерно 7000 км/ч, что даёт нам подлётное время в 17 минут, а полное время устаревания данных – 23 минуты. У «Кинжала» есть радиопрозрачный обтекатель на носу, но он маленький, значит, и РЛС очень небольшая, с учётом того, что условия работы этой маленькой антенны очень тяжёлые (плазма), получаем довольно небольшую зону обнаружения цели, небольшую дальность обнаружения и жёсткие требования к её выводу на цель. А сколько корабль пройдёт за 23 минуты по прямой? На 24 узлах, например, он пройдёт 17 километров. В любую сторону от НМЦ. То есть диаметр ОВМЦ у нас будет 34 километра и в этой зоне будет 300-метровый корабль.
Не выходит у «Кинжала» вот так просто взять и попасть куда надо… И у «Циркона» будут похожие проблемы.
Более того, в наших примерах не учтён фактор РЭБ. Проблема в том, что РЭБ, даже в случае, когда ГСН ПКР может отстроиться от части помех, сильно сужает полосу обзора, то есть «табличные» данные о её ширине резко теряют актуальность, кроме того, страдает дальность обнаружения цели ракетой, она также сокращается до считаных километров (без РЭБ – десятки километров). В таких условиях нужно вывести ракету буквально на сам корабль, а не куда-то в сторону, с обнаружением цели «на краю» полосы обзора ГСН.
Конечно, в ряде ракет реализован режим «наведения на помеху», но у вероятного противника есть системы типа Nulka, у которых излучатель помех летит в стороне от корабля, а ещё есть станции РЭБ на вертолётах, и отвести ракету он сможет. Спасло бы включение ГСН непосредственно перед целью, но ракета должна точно на эту цель выйти.
Так что, выходит, что в НМЦ стрелять нельзя? Можно, но на короткие расстояния, когда цель гарантированно не уйдёт из полосы обзора ГСН ракеты никаким курсом. На десятки километров дальности.
А вот для точной стрельбы на среднюю и большую дальности, то есть на сотни километров, нужны ещё кое-какие данные.
Что, если мы будем знать курс, которым идёт цель? Или какой манёвр она выполняет? Тогда наша ситуация меняется, теперь ОВМЦ становится несоизмеримо меньше, она фактически сводится к погрешности, с которой определён курс.
А если мы знаем ещё и скорость цели? Тогда всё ещё лучше. Теперь огромная неопределённость в положении цели становится пренебрежимо малой.
Курс и скорость цели называются её параметрами движения — ПДЦ.
Применительно к подводной войне говорят «элементы движения цели» (ЭДЦ), и в них ещё входит глубина, но этот вопрос мы трогать не будем.
Если мы определим ПДЦ, то сможем спрогнозировать то место, в котором цель будет к моменту подлёта ракеты. Мы просто проведём экстраполяцию курса с учётом известной скорости и банально отправим ракету туда, где цель будет через те самые 20 минут из прошлого примера.
Схематически это можно определить вот так:
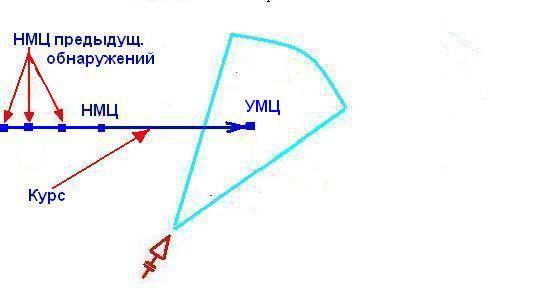
Указанное на схеме прогнозируемое место цели называется "Упреждённое место цели" — УМЦ.
На этой схеме не указана погрешность, и из неё не следует явным образом то, что курс носит вероятностный характер: цель может просто развернуться в момент пуска, а мы на это не можем повлиять. Но так уже намного лучше.
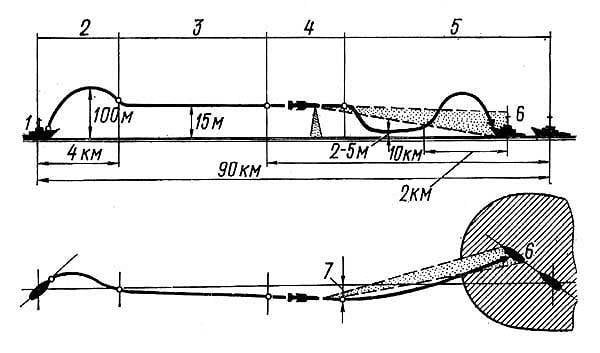
А если мы знаем только курс цели (примерно, как и всё на войне), но не скорость, а надо стрелять? Тогда можно попытаться пустить ракету под таким углом к предполагаемому курсу, чтобы ракета с максимальной вероятностью «встретилась» с целью в каком-то месте.
Это место называется расчётным местом цели – РМЦ.
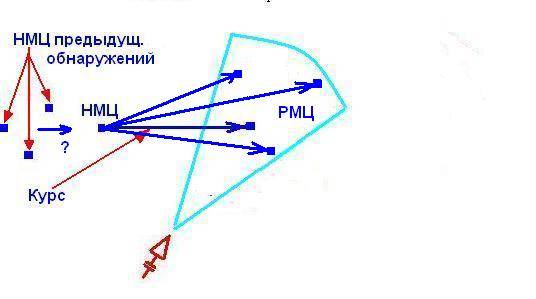
Стрельба в ОВМЦ является исключительным случаем, «Правила ракетной стрельбы» требуют стрелять в НМЦ, УМЦ или РМЦ, причём обеспечив высокую вероятность поражения цели. При этом, как мы видели ранее, стрельба в НМЦ (без знания ПДЦ) возможна с заданной вероятностью попадания только на небольшие дистанции, а стрельба в УМЦ и РМЦ требует знания о цели куда большего объёма информации, чем её координаты на какой-то момент времени.
Эти два вида стрельбы ракетами на большие расстояния требуют знать ПДЦ – курс и скорость (для УМЦ), а желательно ещё и знать, что цель делает (как маневрирует). И всё это с погрешностями и вероятностями. И с поправками на ветер, конечно же.
И вот тогда-то и появляется возможность отправить ракеты туда, где цель будет в нужный момент времени. Это не гарантирует уничтожения цели – она, в конце концов, будет отстреливаться. Но, по крайней мере, ракеты придут туда, куда надо.
Но как узнать курс и скорость цели?
Достаточная информация
Вернёмся к ситуации с ПКР на самодельной береговой ПУ и катером-разведчиком. Допустим, дальность до цели такова, что наша старая дозвуковая ракета с «мёртвой» древней ГСН имеет очень малые шансы достать цель, стреляя по полученному на НМЦ пеленгу (фактически речь идёт о стрельбе в ОВМЦ). Тогда нам надо знать УМЦ. А для этого надо узнать курс и скорость корабля.
Сделаем допущение: у нашего катера-разведчика есть оптический дальномер, а сам он под нейтральным флагом и как опасная цель противником не классифицируется. Тогда, имея дальномер, наш катер произведёт серию замеров дальности до корабля-цели в течение, например, 15 минут, а заодно по углу поворота дальномера на катере вычислит скорость цели.
Переданные по радио на берег данные мы наносим на планшет, и вот оно – УМЦ.
Но для этого оказалось необходимо с катера наблюдать корабль-цель 15 минут и передавать по радио данные на берег, не спугнув противника. Легко представить себе, насколько сложно это будет в ходе реальной войны, когда обнаруженный противником корабль или самолёт немедленно атакуется, а сам противник предпринимает всё возможное для того, чтобы его просто никто не увидел.
И да, спутник с его скоростью замерять ПДЦ в течение 5-15 минут не сможет тоже.
Сделаем промежуточный вывод: для получения всех необходимых данных для ракетной стрельбы на большое расстояние цель должна регулярно и с короткими интервалами (а ещё лучше непрерывно) отслеживаться до момента пуска по ней ракет с передачей данных о цели на носитель ракетного оружия. Только тогда появляется возможность получить все необходимые данные для стрельбы ракетой. Если это условие не выполняется, то вероятность поражения цели резко падает, в том числе до пренебрежимо малых величин (в зависимости от ситуации). А ещё один важный вывод: какой бы дальностью ни обладали ПКР, чем ближе их носитель к цели, тем выше вероятность её поражения.
Просто потому, что данные в реальной войне всегда будут неполными, всегда будет не хватать информации, РЭБ будет «сбивать» наведение, а малое подлётное время хоть как-то может способствовать тому, чтобы ОВМЦ не выросла за полосу обзора ГСН противокорабельной ракеты, особенно в полосу, «зарезанную» помехами противника.
Жаль, что Розовый Пони не дочитал до этого момента.
Разобравшись с тем, какие данные нужны, разберёмся теперь с тем, что же всё-таки такое это ЦУ.
Целеуказание
Если открыть определение Минобороны, которое сделано доступным для широких кругов общества, то словом "целеуказание" называется следующее:
Это «в общем». Под это определение попадает даже огонь «трассерами» по окну с огневой точкой, которую ведёт 24-летний командир мотострелкового взвода, чтобы показать взводу цель. Нас интересует морская составляющая, поэтому уберём из определения всё, что к ней не относится.
Какой вывод следует даже из этого, «размытого» определения? Целеуказание — это фактически ПРОЦЕСС ПЕРЕДАЧИ И ВЫРАБОТКИ ДАННЫХ с параметрами, необходимыми для эффективного применения оружия. В каком виде передаются данные? «В общем случае» — хоть флажными сигналами, но в отечественном флоте и морской авиации давно принято за основной вариант, что ЦУ передаётся с «разведчика» на «носитель» в виде машинных данных специальных комплексов целеуказания.
Для эффективного применения оружия нам мало того что надо обнаружить цель и получить НМЦ, мало того что надо определить её ПДЦ (для чего за целью надо некоторое время следить), мало рассчитать все погрешности, нужно ещё и преобразовать всё это в машинный формат и передать на носители в готовом к применению виде.
Более того, с учётом того, что «разведчик» — это, как правило (хоть и не всегда), самолёт с ограниченным экипажем и высокой уязвимостью от зенитного огня, то там и процесс формирования данных должен быть полностью или частично автоматизирован.
Если же речь идёт о передачи данных иным способом, то это возможно только через какой-то наземный КП с соответствующим временем устаревания данных.
Конечно, на корабль можно передать данные даже голосом, и если они точные, то личный состав БЧ-2 подготовит все данные для стрельбы, отталкиваясь от реального положения своего корабля, введёт их в систему управления ракетным оружием, где они будут преобразованы в то самое «машинное» ЦУ и загружены в ракету или ракеты.
Но это на корабле. В авиации лётчики выводят самолёт в атаку на скорости куда больше, чем скорость звука, под огнём как с надводных кораблей, так и с вражеских перехватчиков, с потерями в составе ударной группы и соответствующей обстановкой в радиоэфире, в сложнейшей помеховой обстановке, и вот там сидеть с линейками и вычислителями и что-то куда-то подгружать просто некогда. Наложив на это несовершенство приборов отображения информации о цели и кислородное голодание (иногда), получаем обстановку, в которой люди действуют на пределе человеческих возможностей, на грани. Соответственно, нужен "машинный формат".
Длительное время ЦУ для авиации означало не передачу и получение данных для пуска ракеты, а передачу и получение данных, нужных для выхода самолёта на рубеж её пуска – захват цели ракета производила непосредственно ещё на носителе.
С появлением на самолетах таких ракет, как Х-35, появилась возможность атаковать цели «по-корабельному» — с захватом цели ГСН ракеты на курсе, уже после отцепа от носителя. Но жёсткость требований к ЦУ это не снижает, а наоборот, повышает. Ошибку после отцепа ракеты уже не исправить, но у пилотов «старой» авиации была возможность «показать» ракете цель до пуска, исправив последствия выхода на цель по неточным данным ЦУ путём целеуказания ракете по выбранной для поражения цели непосредственно с самолетной РЛС. Современные пилоты могут пускать ракеты, не наблюдая цель с помощью собственной РЛС, и это один из штатных способов их применения. Значит, и данные ЦУ должны быть точнее.
И вот теперь, понимая всю сложность проблемы, зададим себе вопрос: а как вообще можно получить все данные? Естественно, в реальной войне, где противник отстреливает авиаразведку и давит связь помехами?
Разберём этот вопрос для начала на примере комплекса «Кинжал».
Реальности «Кинжала»
Представим себе, что нам понадобилось было бы для того, чтобы всё-таки попасть по морской цели этой ракетой. Итак, полуслепая от плазмы антенна под маленьким радиопрозрачным обтекателем «Кинжала» должна оказаться очень близко к кораблю, так, чтобы ни проблемы с наведением, обусловленные скоростью, ни РЭБ просто не успели бы помешать ракете. Что для этого нужно? Нужно предельно точно передать на носитель ЦУ с упреждённым местом цели, почти без погрешностей, настолько точно, чтобы «Кинжал» мог попасть в цель даже вообще без наведения.








